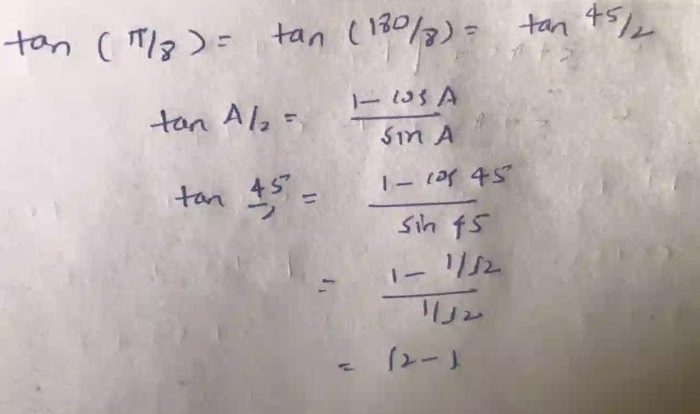Embark on a mathematical odyssey with Big Ideas Math Answers Algebra 2 Chapter 1, a comprehensive guide that illuminates the foundational concepts of algebra. This chapter lays the groundwork for a deeper understanding of functions, equations, inequalities, and their applications in the real world.
Prepare to delve into the intricacies of linear and quadratic equations, unravel the mysteries of functions and their graphs, and explore the techniques for solving systems of equations and inequalities. With clear explanations, detailed examples, and engaging real-world scenarios, this chapter will transform you into an algebra aficionado.
Key Concepts and Definitions

Chapter 1 of Big Ideas Math Algebra 2 introduces fundamental concepts that lay the foundation for the study of algebra. These concepts include functions, equations, and inequalities, each playing a crucial role in understanding algebraic relationships and solving problems.
Functions
A function is a relation that assigns to each element of a set (called the domain) exactly one element of another set (called the range). Functions are represented using various notations, including the function notation f(x), where x is the independent variable and f(x) is the dependent variable.
Equations
An equation is a statement that two mathematical expressions are equal. Equations can be linear, quadratic, or polynomial, depending on the highest power of the variable involved. Solving equations involves finding the values of the variable that make the equation true.
Inequalities
An inequality is a statement that two mathematical expressions are not equal. Inequalities can be linear, quadratic, or polynomial, and they represent relationships where one expression is greater than, less than, or not equal to another expression. Solving inequalities involves finding the values of the variable that satisfy the inequality.
Solving Equations and Inequalities: Big Ideas Math Answers Algebra 2 Chapter 1
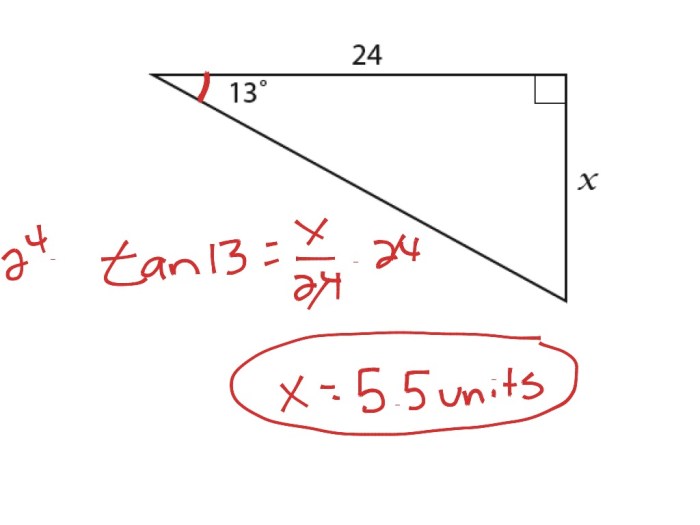
Chapter 1 of Big Ideas Math Algebra 2 covers various methods for solving equations and inequalities. These methods include substitution, elimination, and graphing.
Solving Linear Equations
- Substitution: Replace the variable with a known value to find the solution.
- Elimination: Add or subtract equations to eliminate variables and solve for the remaining variable.
- Graphing: Plot the equation on a graph and find the point where it crosses the x-axis (for x-intercepts) or y-axis (for y-intercepts).
Solving Quadratic Equations
- Factoring: Factor the quadratic expression and set each factor equal to zero to find the solutions.
- Completing the Square: Convert the quadratic expression into a perfect square trinomial and find the solutions using square roots.
- Quadratic Formula: Use the quadratic formula to find the solutions directly.
Solving Inequalities
Solving inequalities involves finding the values of the variable that satisfy the inequality. This can be done by graphing the inequality or by using algebraic methods, such as multiplying or dividing both sides by the same negative number.
Functions and Their Graphs
Chapter 1 of Big Ideas Math Algebra 2 introduces the concept of functions and their graphs. Functions can be linear, quadratic, or absolute value functions, each with its own unique characteristics and graphical representations.
Linear Functions
Linear functions are functions whose graphs are straight lines. They can be represented by the equation y = mx + b, where m is the slope and b is the y-intercept.
Quadratic Functions
Quadratic functions are functions whose graphs are parabolas. They can be represented by the equation y = ax^2 + bx + c, where a, b, and c are constants.
Absolute Value Functions
Absolute value functions are functions whose graphs are V-shaped. They can be represented by the equation y = |x|, where x is the independent variable.
Key Features of Functions
- Intercepts: The points where the graph crosses the x-axis (x-intercepts) or y-axis (y-intercepts).
- Slope: The steepness of the line for linear functions.
- Vertex: The highest or lowest point of a parabola for quadratic functions.
- Asymptotes: Vertical or horizontal lines that the graph approaches but never touches.
Systems of Equations and Inequalities

Chapter 1 of Big Ideas Math Algebra 2 covers methods for solving systems of equations and inequalities. Systems involve two or more equations or inequalities that must be solved simultaneously.
Systems of Linear Equations
- Substitution: Solve one equation for a variable and substitute it into the other equation.
- Elimination: Add or subtract equations to eliminate variables and solve for the remaining variables.
- Matrices: Use matrices to represent the system and solve for the variables using matrix operations.
Systems of Inequalities
Solving systems of inequalities involves finding the region of the plane that satisfies all the inequalities. This region is called the solution region.
Applications of Algebra
Chapter 1 of Big Ideas Math Algebra 2 highlights the applications of algebra in various fields, including science, engineering, and finance.
Science
- Modeling physical phenomena, such as motion and projectile motion.
- Solving problems in chemistry, such as balancing chemical equations.
Engineering, Big ideas math answers algebra 2 chapter 1
- Designing structures and systems, such as bridges and electrical circuits.
- Solving problems in fluid mechanics and thermodynamics.
Finance
- Calculating interest rates and loan payments.
- Modeling financial markets and investments.
Query Resolution
What are the key concepts covered in Big Ideas Math Algebra 2 Chapter 1?
Chapter 1 introduces the fundamental concepts of algebra, including functions, equations, inequalities, and their applications.
How can I solve linear equations and inequalities?
The chapter provides step-by-step methods for solving linear equations using substitution, elimination, and graphing, as well as techniques for solving linear and absolute value inequalities.
What is the concept of a function and how do I graph it?
Chapter 1 defines the concept of a function and its domain and range. It also explains how to graph linear, quadratic, and absolute value functions, highlighting their key features.
How can I solve systems of equations and inequalities?
The chapter presents various methods for solving systems of linear equations, including substitution, elimination, and matrices. It also discusses the concept of solving systems of inequalities and graphing the solution region.
What are the real-world applications of algebra?
Chapter 1 explores how algebraic concepts are applied in various fields, such as science, engineering, and finance, demonstrating the importance of algebra as a foundation for higher-level mathematics and STEM disciplines.