Special segments in triangles worksheet – Embarking on a journey to unravel the intricacies of special segments in triangles, this worksheet delves into the heart of geometry, exploring the fundamental concepts, properties, and applications of these essential elements. Prepare to expand your understanding and sharpen your geometric skills as we embark on this captivating exploration.
Special segments, including medians, altitudes, perpendicular bisectors, and angle bisectors, hold the key to unlocking a wealth of geometric insights. This comprehensive worksheet provides a structured approach to grasping these concepts, empowering you to confidently navigate the realm of triangles.
Special Segments in Triangles: Special Segments In Triangles Worksheet
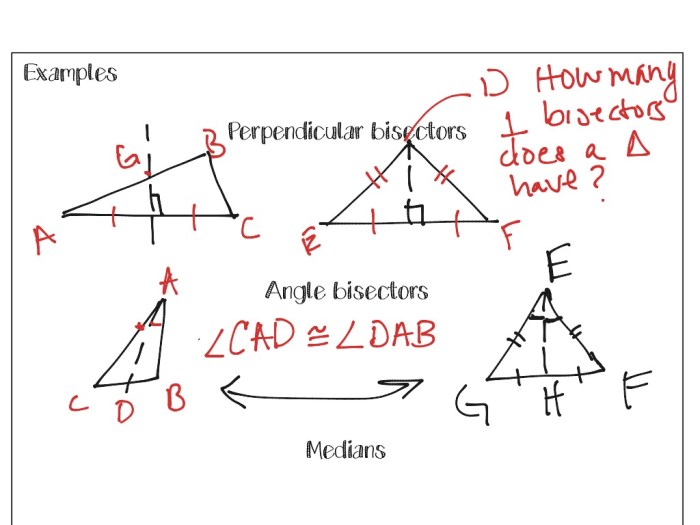
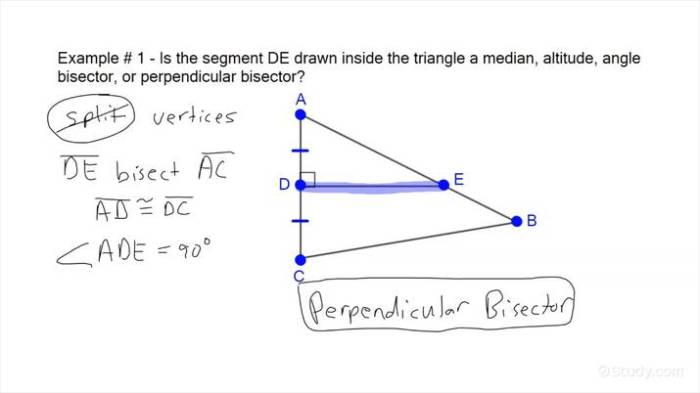
In geometry, special segments are line segments that have specific properties and relationships within a triangle. These segments include medians, altitudes, perpendicular bisectors, and angle bisectors. Understanding these special segments is crucial for solving various problems involving triangles.
Types of Special Segments in Triangles
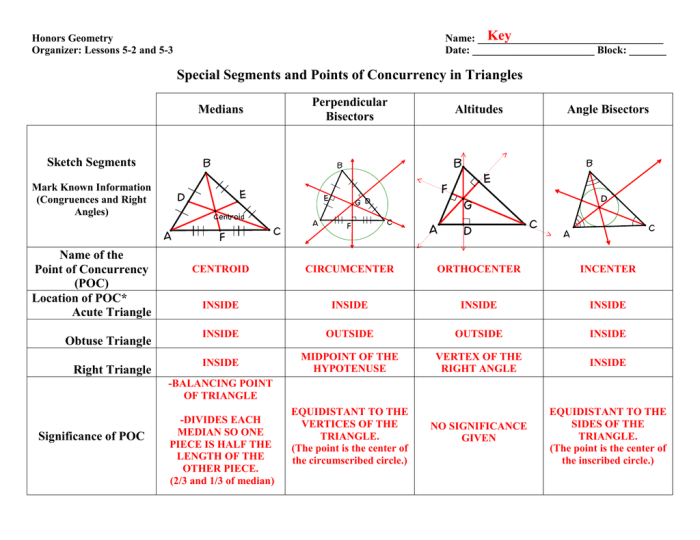
- Medians: A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. Each triangle has three medians.
- Altitudes: An altitude is a line segment that is perpendicular to a side of a triangle and passes through the opposite vertex. Each triangle has three altitudes.
- Perpendicular Bisectors: A perpendicular bisector is a line segment that is perpendicular to a side of a triangle and passes through the midpoint of that side. Each side of a triangle has one perpendicular bisector.
- Angle Bisectors: An angle bisector is a line segment that divides an angle of a triangle into two equal parts. Each angle of a triangle has one angle bisector.
Properties of Special Segments
- Medians:
- Intersect at a point called the centroid, which divides the triangle into two equal areas.
- Divide the triangle into two equal areas.
- Altitudes:
- Perpendicular to the sides of the triangle.
- Intersect at a point called the orthocenter.
- Perpendicular Bisectors:
- Perpendicular to the sides of the triangle.
- Intersect at a point called the circumcenter.
- Angle Bisectors:
- Divide the angles of the triangle into two equal parts.
- Intersect at a point called the incenter.
Applications of Special Segments, Special segments in triangles worksheet
- Finding the Area of a Triangle: The area of a triangle can be calculated using its medians or altitudes.
- Finding the Perimeter of a Triangle: The perimeter of a triangle can be calculated using its perpendicular bisectors.
- Constructing Triangles with Specific Properties: Special segments can be used to construct triangles with specific angles, side lengths, or area.
Key Questions Answered
What is the difference between a median and an altitude?
A median connects a vertex to the midpoint of the opposite side, while an altitude is a perpendicular line segment from a vertex to the opposite side.
How can I use special segments to find the area of a triangle?
The area of a triangle can be found using the formula: Area = (1/2) – base – height, where the height is the length of an altitude.
What is the centroid of a triangle?
The centroid is the point where the three medians of a triangle intersect. It divides the triangle into three equal areas.